A loss function is used to optimize a machine learning algorithm. An accuracy metric is used to measure the algorithm’s performance (accuracy) in an interpretable way. It goes against my intuition that these two sometimes conflict: loss is getting better while accuracy is getting worse, or vice versa.

I’m working on a classification problem and once again got these conflicting results on the validation set.

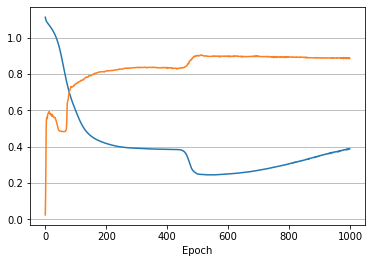
Loss vs Accuracy

Accuracy (orange) finally rises to a bit over 90%, while the loss (blue) drops nicely until epoch 537 and then starts deteriorating. Around epoch 50 there’s a strange drop in accuracy even though the loss is smoothly and quickly getting better.

My loss function here is categorical cross-entropy that is used to predict class probabilities. The target values are one-hot encoded so the loss is the best when the model’s output is very close to 1 for the right category and very close to 0 for other categories. The loss is a continuous variable.

Accuracy or more precisely categorical accuracy gets a discrete true or false value for a particular sample.

It’s easy to construct a concrete test case showing conflicting values. Case 1 has less error but worse accuracy than case 2:

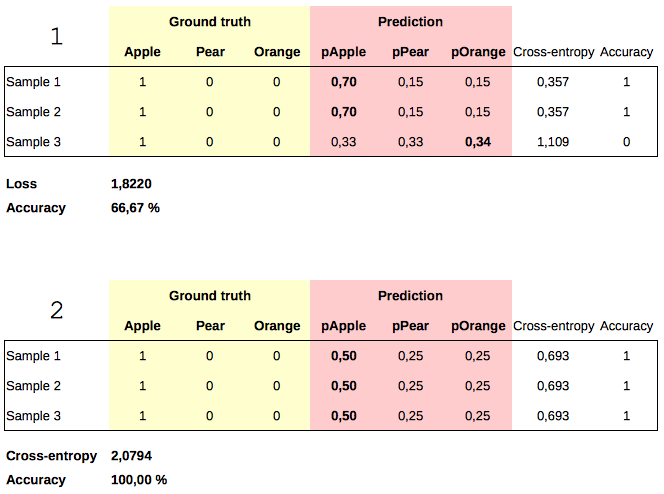
For reference, calculating categorical cross-entropy in Keras for one sample:

truth = K.variable([[1., 0., 0.]])
prediction = K.variable([[.50, .25, .25]])
loss = K.eval(K.categorical_crossentropy(truth, prediction))

In what kind of situations does loss-vs-accuracy discrepancy occur?

• When the predictions get more confident, loss gets better even though accuracy stays the same. The model is thus more robust, as there’s a wider margin between classes.
• If the model becomes over-confident in its predictions, a single false prediction will increase the loss unproportionally compared to the (minor) drop in accuracy. An over-confident model can have good accuracy but bad loss. I’d assume over-confidence equals over-fitting.
• Imbalanced distributions: if 90% of the samples are “apples”, then the model would have good accuracy score if it simply predicts “apple” every time.

Accuracy metric is easier to interprete, at least for categorical training data. Accuracy however isn’t differentiable so it can’t be used for back-propagation by the learning algorithm. We need a differentiable loss function to act as a good proxy for accuracy.